There’s a bridge not far from Brown Bag’s studio in Dublin that everyone in animation should know about.
It’s a pretty unremarkable looking old bridge in the middle of an industrial estate in Cabra, but it hosts a plaque commemorating a flash of genius some consider as the birth of modern (non-commutative) algebra. Hamilton’s discovery of quaternions. We use them in animation to rotate stuff.
Rotations are a big deal in character animation. The skeletons used to make a character move are a collection of bones of a certain length with rotations describing where the bones point. Sure, we use a rig with animator friendly controls on top of that to help make certain things easier but, at the end of the day, the movement of a character all comes down to the rotation values on those joints.
Brown Bag Films are in the rotation business.
“We love Rotation!”

This pose of Henry Hugglemonster is the result of setting 194 rotations.
Animators typically use Euler rotations when animating. In 3d animation an Euler rotation is a set of 3 angles which describe the amount of rotation around the X, Y and Z axes. They are a nice way to visualise rotation, and they usually produce an intuitive set of curves when a rotation is graphed over time. When a director uses the words “pan”, “tilt”, “roll” to help frame up a shot, they’re using Euler rotations. But these rotations have a few issues. Say the phrase “gimbal lock” or “bad rotation interpolation” to a 3D animator and wait for the veins on their forehead to pop. Interestingly a 2d animator's blood pressure is unaffected… Many animation, games and physics software packages now use quaternions to manage rotation (although it may happen deep down internally in the software).
A quaternion allows us to rotate a point around an arbitrary vector. That’s important because it overcomes some of the fundamental limitations with describing a 3d rotation using only 3 numbers, as in Euler rotations. A quaternion is made of 4 numbers (so it is 4 dimensional) - a scalar (number) part and a vector part, and can be written down in a few different ways eg:
q = [w, v]
...or
q = [w, (x, y, z)]
...or (the more old fashioned way)
q = [w + xi + yj + zk]
I’m a pipeline developer not a mathematician, I'll have to leave more thorough explanations to the experts but hopefully I can give a simple description. So for now you could think of the numbers as:
- w being related to the angle to rotate by (divided by 2 and cos’d), and
- v or (x, y, z) being related to the vector to rotate around (times sin(angle/2))
- i, j, k representing the axes of a special coordinate system that the vector lives in. We’ll come back to this part later.
So a more complete way to write down a rotation quaternion is
q = [cos(θ/2), v * sin(θ/2))]
...or even
q = cos(θ/2) + i(x * sin(θ/2)) + j(y * sin(θ/2)) + k(z * sin(θ/2))
To rotate the point P by the quaternion q we multiply q by p by the inverse of q. So the point p is basically sandwiched between 2 quaternions.
p’ = qpq-1
where
- p’ (say “p prime”) holds the new position of p, after it has been rotated
- q is the quaternion
- p is the original 3d point “padded out” into a 4d pure quaternion by sticking a 0 at the front eg [0, x, y, z]. There needs to be 4 components in order to multiply.
- q-1 is the inverse or conjugate of q
It might look a bit unnecessary to also multiply by the inverse quaternion but the reason is to eliminate an unwanted wobble in the rotation. That’s the reason the angle θ is halved in the equations above - we don’t want to double up the rotation. The first multiplication of q gets us halfway there and introduces half the amount of wobble, the inverse of q completes the rotation and eliminates the wobble.
But how are two quaternions multiplied in the first place you ask? Let's get back to the i, j, k vectors from Hamilton's plaque. It's helpful to first understand “complex numbers”, which can be used as a way to rotate in 2d, before looking at how Hamilton expanded on the idea in 3d. If you don’t have time for that, then just accept that a complex number has 2 terms and looks like this (3 + 4i)
Hamilton tried to find a 3d equivalent for the 2d complex number plane by introducing a third term “j”. His eventual realisation is that a fourth term, “k” was also necessary to properly close the product of 2 of these objects (ie multiplying a quaternion by a quaternion should yield a third quaternion). What's more, the order that the i, j, k terms were multiplied was important. When the order is reversed the result is negative! This would be considered a groundbreaking discovery at the time, so it's a good thing he had a nearby bridge to quickly scratch the idea onto as he walked past! So these are the special rules he came up with that day:
i2 = j2 = k2 = ijk = -1
ij = k ji= -k
jk = i kj = -i
ki = j ik = -j
These rules allow us multiply 2 quaternions qa and qb like so: (deep breath!)
|
| Nothing fancy going on here - this is just the “distribution rule” from school. I’ve drawn out the pattern for the last element in case you forgot |
Mmmm look at all those i, j, k terms we can simplify away using the rules above!
|
| In the top row we got rid of all the squared terms (they turned into negatives). In the other rows we’ve just applied the rest of Hamilton’s rules and factored out any remaining i, j, k |
And we are back with something in the form of another quaternion! This multiplication can happen thousands of times every second to produce the motion of an animated character.
These days its more common to use a shorter, easier to read form by writing the quaternions in [w, v] style and using vector dot and cross product (which under the hood still follows the anti-commutative rules of Hamilton’s multiplication). I left out this representation to not make things more confusing than they already are! After all this blog post is really just to help understand what is written on the bridge!

The bridge itself, Broombridge, has become almost a pilgrimage for mathematicians the world over, and is just a 30 minute walk from the city along the Royal Canal. The swans can be a little overly friendly though!
Luke Harris
We Love Animation®
Brown Bag Labs is an exciting online space, brought to you by Brown Bag Films. We share great content for families as well as behind the scenes fun and tutorials from the Brown Bag Films team.



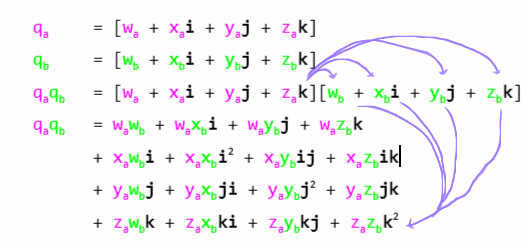
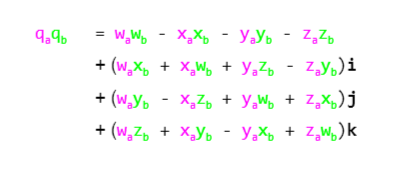
Get our great newsletter!
Get our great newsletter!